[Paper reading] Implicit Neural Representations
2023. 9. 18. 12:32ㆍArtificialIntelligence/PaperReading
Implicit Neural Representations with Periodic Activation Functions

Abstract
- Implicitly defined, continuous, differentiable signal representations parameterized by neural networks have emerged as a powerful paradigm, offering many possible benefits over conventional representations.
- However, current network architectures for such implicit neural representations are incapable of modeling signals with fine detail, and fail to represent a signal’s spatial and temporal derivatives, despite the fact that these are essential to many physical signals defined implicitly as the solution to partial differential equations.
- We propose to leverage periodic activation functions for implicit neural representations and demonstrate that these networks, dubbed sinusoidal representation networks or SIRENs, are ideally suited for representing complex natural signals and their derivatives.
- We analyze SIREN activation statistics to propose a principled initialization scheme and demonstrate the representation of images, wavefields, video, sound, and their derivatives. Further, we show how SIRENs can be leveraged to solve challenging boundary value problems, such as particular Eikonal equations (yielding signed distance functions), the Poisson equation, and the Helmholtz and wave equations.
- Lastly, we combine SIRENs with hypernetworks to learn priors over the space of SIREN functions. Please see the project website for a video overview of the proposed method and all applications.
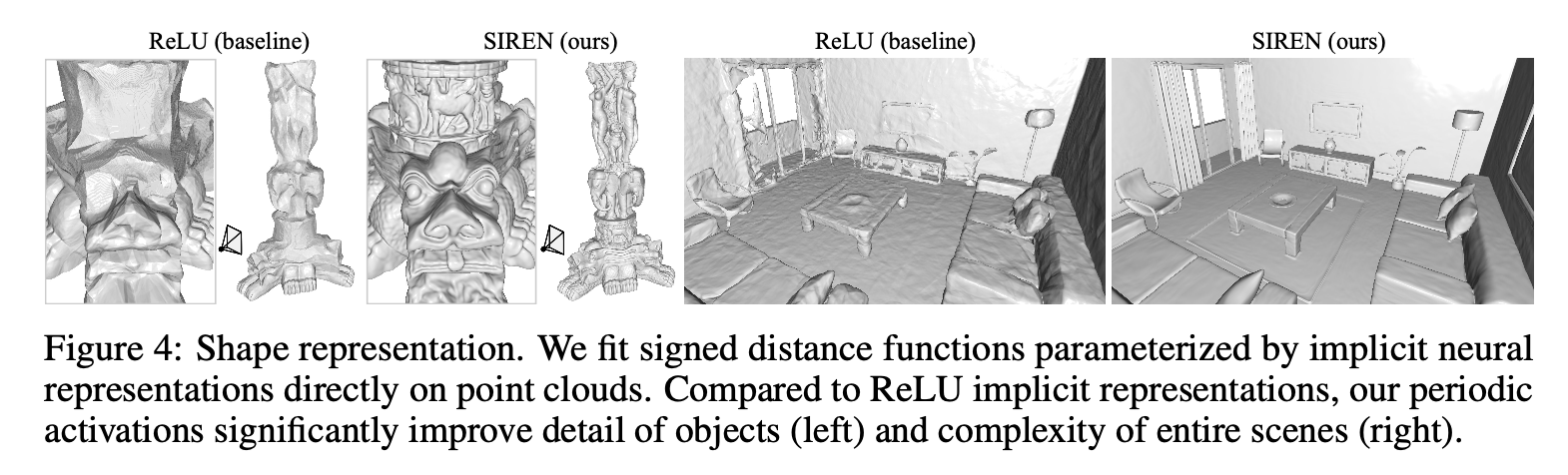
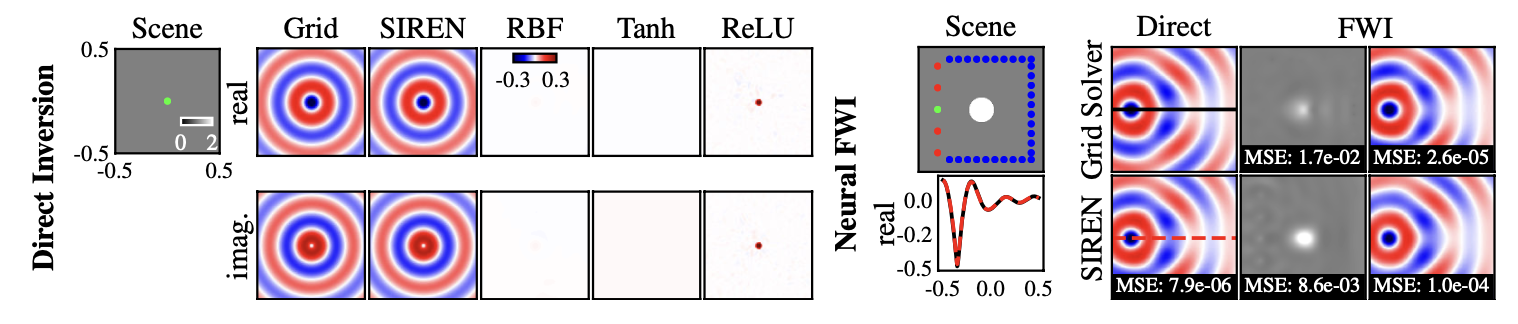
Discussion and Conclusion
- The question of how to represent a signal is at the core of many problems across science and engineering.
- Implicit neural representations may provide a new tool for many of these by offering a number of potential benefits over conventional continuous and discrete representations. We demonstrate that periodic activation functions are ideally suited for representing complex natural signals and their derivatives using implicit neural representations.
- We also prototype several boundary value problems that our framework is capable of solving robustly. There are several exciting avenues for future work, including the exploration of other types of inverse problems and applications in areas beyond implicit neural representations, for example neural ODEs. With this work, we make important contributions to the emerging field of implicit neural representation learning and its applications.
'ArtificialIntelligence > PaperReading' 카테고리의 다른 글
| [Paper reading] NeRF, Representing Scenes as Neural Radiance Fields for View Synthesis (0) | 2023.09.24 |
|---|---|
| [Paper reading] Denoising Diffusion Probabilistic Models (0) | 2023.09.19 |
| [Paper reading] Dataset Condensation Keynote (0) | 2023.09.11 |
| [Paper reading] Dataset Condensation reading (0) | 2023.09.11 |
| [Paper reading] Dataset Condensation Summary (0) | 2023.09.10 |