[Paper reading] NeRF, Representing Scenes as Neural Radiance Fields for View Synthesis
2023. 9. 24. 20:08ㆍArtificialIntelligence/PaperReading
Abstract
Keywords: scene representation, view synthesis, image-based rendering, volume rendering, 3D deep learning
- We present a method that achieves state-of-the-art results for synthesizing novel views of complex scenes by optimizing an underlying continuous volumetric scene function using a sparse set of input views.
- Our algorithm represents a scene using a fully-connected (non- convolutional) deep network, whose input is a single continuous 5D coordinate (spatial location (x, y, z) and viewing direction (θ, φ)) and whose output is the volume density and view-dependent emitted radiance at that spatial location.
- We synthesize views by querying 5D coordinates along camera rays and use classic volume rendering techniques to project the output colors and densities into an image. Because volume rendering is naturally differentiable, the only input required to optimize our representation is a set of images with known camera poses.
- We describe how to effectively optimize neural radiance fields to render photorealistic novel views of scenes with complicated geometry and appearance, and demonstrate results that outperform prior work on neural rendering and view synthesis. View synthesis results are best viewed as videos, so we urge readers to view our supplementary video for convincing comparisons.

Introduction
- In this work, we address the long-standing problem of view synthesis in a new way by directly optimizing parameters of a continuous 5D scene representation to minimize the error of rendering a set of captured images.
- We represent a static scene as a continuous 5D function that outputs the radiance emitted in each direction (θ,φ) at each point (x,y,z) in space, and a density at each point which acts like a differential opacity controlling how much radiance is accumulated by a ray passing through (x, y, z).
- Our method optimizes a deep fully-connected neural network without any convolutional layers (often referred to as a multilayer perceptron or MLP) to represent this function by regressing from a single 5D coordinate (x,y,z,θ,φ) to a single volume density and view-dependent RGB color.
- To render this neural radiance field (NeRF) from a particular viewpoint we:
1) march camera rays through the scene to generate a sampled set of 3D points
2) use those points and their corresponding 2D viewing directions as input to the neural network to produce an output set of colors and densities
3) use classical volume rendering techniques to accumulate those colors and densities into a 2D image. - Because this process is naturally differentiable, we can use gradient descent to optimize this model by minimizing the error between each observed image and the corresponding views rendered from our representation. Minimizing this error across multiple views encourages the network to predict a coherent model of the scene by assigning high volume densities and accurate colors to the locations that contain the true underlying scene content.
해당 방법론의 의의
- Our approach inherits the benefits of volumetric representations: both can represent complex real-world geometry and appearance and are well suited for gradient-based optimization using projected images.
- Crucially, our method overcomes the prohibitive storage costs of discretized voxel grids when modeling complex scenes at high-resolutions.
- In summary, our technical contributions are:
– An approach for representing continuous scenes with complex geometry and materials as 5D neural radiance fields, parameterized as basic MLP networks.
– A differentiable rendering procedure based on classical volume rendering techniques, which we use to optimize these representations from standard RGB images. This includes a hierarchical sampling strategy to allocate the MLP’s capacity towards space with visible scene content.
– A positional encoding to map each input 5D coordinate into a higher dimensional space, which enables us to successfully optimize neural radiance fields to represent high-frequency scene content.
- We demonstrate that our resulting neural radiance field method quantitatively and qualitatively outperforms state-of-the-art view synthesis methods, including works that fit neural 3D representations to scenes as well as works that train deep convolutional networks to predict sampled volumetric representations.
- As far as we know, this paper presents the first continuous neural scene representation that is able to render high-resolution photorealistic novel views of real objects and scenes from RGB images captured in natural settings.

Volume Rendering with Radiance Fields
- Our 5D neural radiance field represents a scene as the volume density and directional emitted radiance at any point in space. We render the color of any ray passing through the scene using principles from classical volume rendering.
- The volume density σ(x) can be interpreted as the differential probability of a ray terminating at an infinitesimal particle at location x.
- The expected color C(r) of camera ray r(t) = o + td with near and far bounds tn and tf is

- The function T(t) denotes the accumulated transmittance along the ray from tn to t,
- i.e., the probability that the ray travels from tn to t without hitting any other particle.
- Rendering a view from our continuous neural radiance field requires estimating this integral C(r) for a camera ray traced through each pixel of the desired virtual camera.

- Our neural radiance field representation outputs RGB color as a 5D function of both spatial position x and viewing direction d.
- Here, we visualize example directional color distributions for two spatial locations in our neural representation of the Ship scene.
- In (a) and (b), we show the appearance of two fixed 3D points from two different camera positions
one on the side of the ship (orange insets) and one on the surface of the water (blue insets). - Our method predicts the changing specular appearance of these two 3D points, and in (c) we show how this behavior generalizes continuously across the whole hemisphere of viewing directions.
Conclusion
- Our work directly addresses deficiencies of prior work that uses MLPs to represent objects and scenes as continuous functions. We demonstrate that representing scenes as 5D neural radiance fields (an MLP that outputs volume density and view-dependent emitted radiance as a function of 3D location and 2D viewing direction) produces better renderings than the previously-dominant approach of training deep convolutional networks to output discretized voxel representations.
- Although we have proposed a hierarchical sampling strategy to make rendering more sample-efficient (for both training and testing), there is still much more progress to be made in investigating techniques to efficiently optimize and render neural radiance fields.
- Another direction for future work is interpretability: sampled representations such as voxel grids and meshes admit reasoning about the expected quality of rendered views and failure modes, but it is unclear how to analyze these issues when we encode scenes in the weights of a deep neural network. We believe that this work makes progress towards a graphics pipeline based on real world imagery, where complex scenes could be composed of neural radiance fields optimized from images of actual objects and scenes.
장점
- We find that the basic implementation of optimizing a neural radiance field representation for a complex scene does not converge to a sufficiently high resolution representation and is inefficient in the required number of samples per camera ray. (기존의 문제점)
- We address these issues by transforming input 5D coordinates with a positional encoding that enables the MLP to represent higher frequency functions, and we propose a hierarchical sampling procedure to reduce the number of queries required to adequately sample this high-frequency scene representation.
- 문제점을 해결하기 위해, 방법론이 제시된 과정이 논리적으로 해결된 것 같아서 좋았다.
Question
- quadrature, 구적법에 관한 이야기가 나오는데, 이 부분이 잘 이해되지 않았다.
- We numerically estimate this continuous integral using quadrature.
- Deterministic quadrature, which is typically used for rendering discretized voxel grids, would effectively limit our representation’s resolution because the MLP would only be queried at a fixed discrete set of locations.
- Instead, we use a stratified sampling approach where we partition [tn, tf] into N evenly-spaced bins and then draw one sample uniformly at random from within each bin
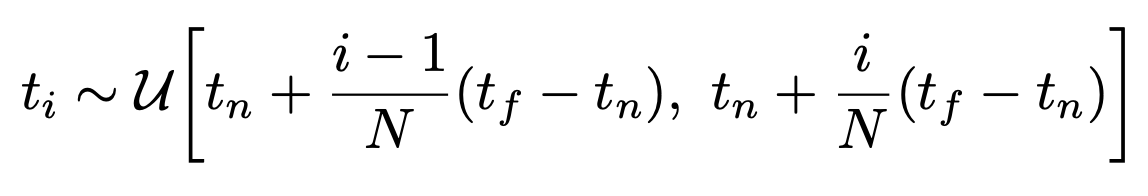
'ArtificialIntelligence > PaperReading' 카테고리의 다른 글
| [Paper reading] Dataset Condensation with Distribution Matching (1) | 2023.10.01 |
|---|---|
| [Paper reading] Denoising Diffusion Probabilistic Models (0) | 2023.09.19 |
| [Paper reading] Implicit Neural Representations (0) | 2023.09.18 |
| [Paper reading] Dataset Condensation Keynote (0) | 2023.09.11 |
| [Paper reading] Dataset Condensation reading (0) | 2023.09.11 |