2023. 10. 1. 22:13ㆍArtificialIntelligence/PaperReading
Dataset Condensation with Distribution Matching
Abstraction
- Computational cost of training state-of-the-art deep models in many learning problems is rapidly increasing due to more sophisticated models and larger datasets. A recent promising direction for reducing training cost is dataset condensation that aims to replace the original large training set with a significantly smaller learned synthetic set while preserving the original information.
- While training deep models on the small set of condensed images can be extremely fast, their synthesis remains computationally expensive due to the complex bi-level optimization and second- order derivative computation.
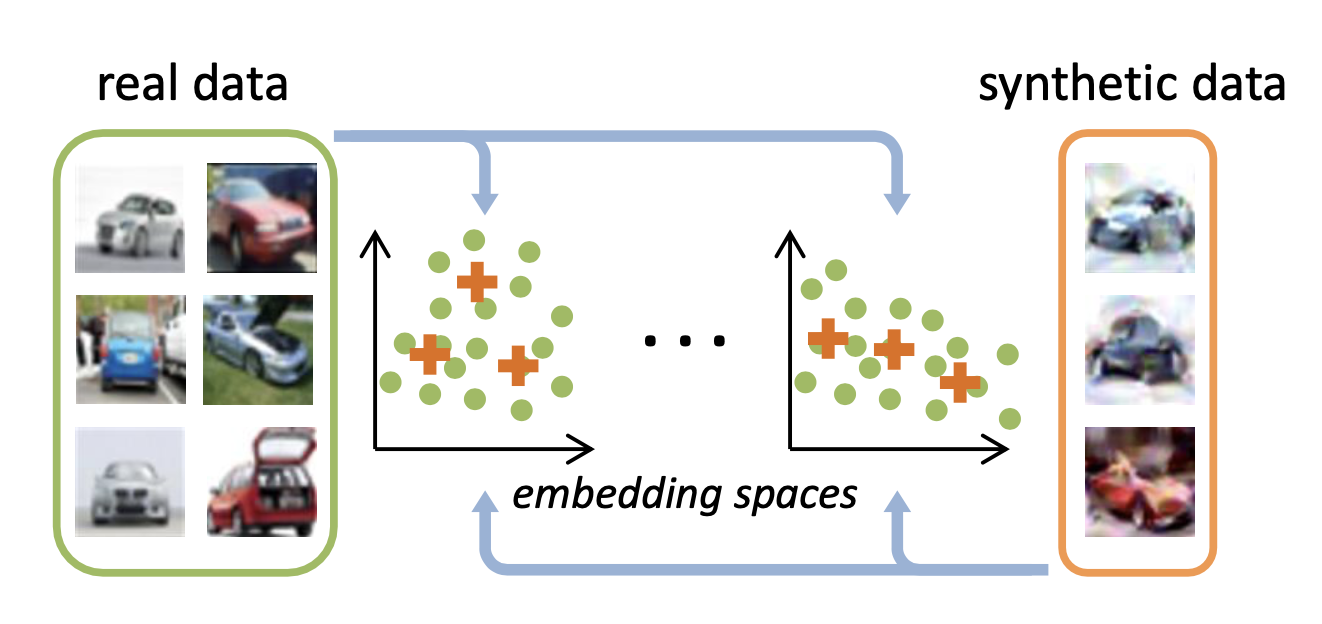
- In this work, we propose a simple yet effective method that synthesizes condensed images by matching feature distributions of the synthetic and original training images in many sampled embedding spaces.
- Our method significantly reduces the synthesis cost while achieving comparable or better performance. Thanks to its efficiency, we apply our method to more realistic and larger datasets with sophisticated neural architectures and obtain a significant performance boost1. We also show promising practical benefits of our method in continual learning and neural architecture search.
Dataset Condensation with Distribution Matching
- Our goal is to synthesize data that can accurately approximate the distribution of the real training data in a similar spirit to coreset techniques. However, to this end, we do not limit our method to select a subset of the training samples but to synthesize them.
- As the training images are typically very high dimensional, estimating the real data distribution PD can be expensive and inaccurate.
- Instead, we assume that each training image x can be embedded into a lower dimensional space by using a family of parametric functions ψ (d를 d'으로 매핑) where d′ ≪ d and θ is the parameter.
- In other words, each embedding function ψ can be seen as providing a partial interpretation of its input, while their combination provides a complete one. Now we can estimate the distance between the real and synthetic data distribution with commonly used maximum mean discrepancy (MMD) where H is reproducing kernel Hilbert space.

- As we do not have access to ground-truth data distributions, we use the empirical estimate of the MMD
- Pθ is the distribution of network parameters

- We also apply the differentiable Siamese augmentation A(·,ω) to real and synthetic data that implements the same randomly sampled augmentation to the real and synthetic minibatch in training, where ω ∼ Ω is the augmentation parameter such as the rotation degree. (DSA?)
- Thus, the learned synthetic data can benefit from semantic- preserving transformations (e.g. cropping) and learn prior knowledge about spatial configuration of samples while training deep neural networks with data augmentation. Finally, we solve the following optimization problem
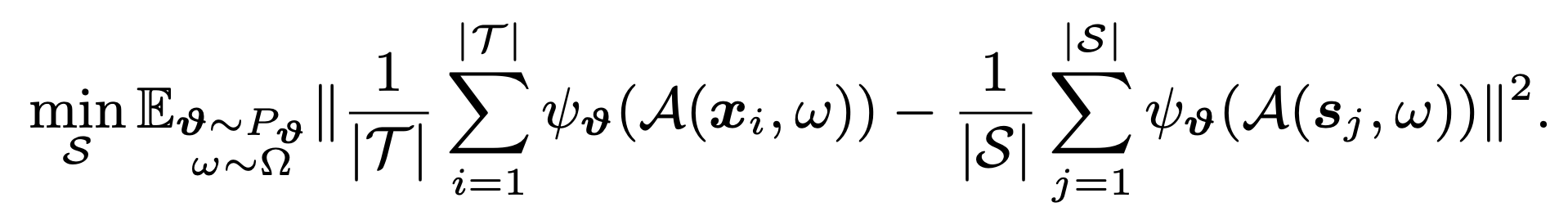
- We learn the synthetic data S by minimizing the discrepancy between two distributions in various embedding spaces by sampling θ. Importantly eq. (6) can be efficiently solved, as it requires only optimizing S but no model parameters and thus avoids expensive bi-level optimization. This is in contrast to the existing formulations that involve bi-level optimizations over network parameters θ and the synthetic data S.
- Note that, as we target at image classification problems, we minimize the discrepancy between the real and synthetic samples of the same class only. We assume that each real training sample is labelled and we also set a label to each synthetic sample and keep it fixed during training.

Conclusion
- In this paper, we propose an efficient dataset condensation method based on distribution matching.
- To our knowledge, it is the first solution that has neither bi-level optimization nor second-order derivative. Thus, the synthetic data of different classes can be learned independently and in parallel. Thanks to its efficiency, we can apply our method to more challenging datasets - TinyImageNet and ImageNet-1K, and learn larger synthetic sets - 1250 im- ages/class on CIFAR10.
- Our method is 45 times faster than the state-of-the-art for learning 50 images/class synthetic set on CIFAR10. We also empirically prove that our method can produce more informative memory for continual learning and better proxy set for speeding up model evaluation in NAS.
- Though remarkable progress has been seen in this area since the pioneering work [46] released in 2018, dataset condensation is still in its early stage. We will extend dataset condensation to more complex vision tasks in the future.
Code Review
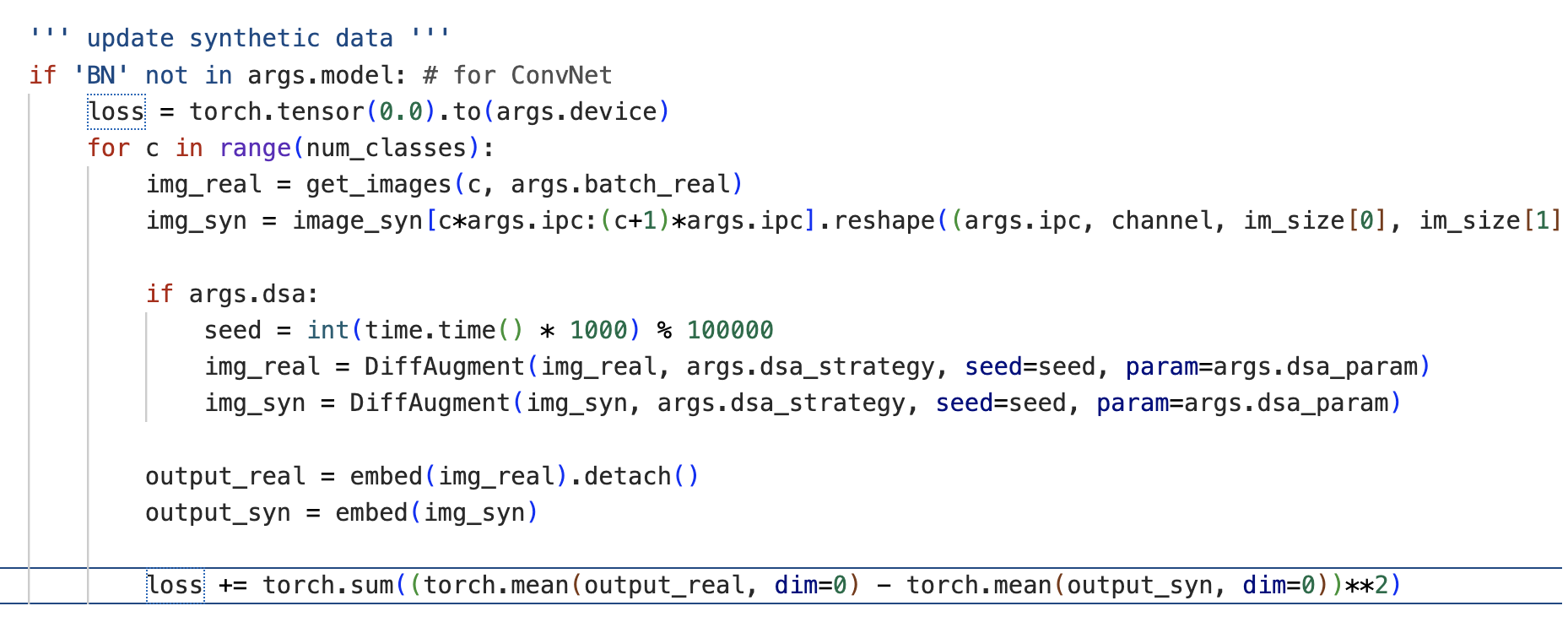
해당 메소드가 어떻게 반영되는 지 궁금하여, loss 및 update 코드를 찾아보았다! :)

- 참고로 Dataset Condensation with Gradient Matching과 동일한 git-hub repository에 main_DM.py로 distribution matching이 구현되어있다.
- gradient 사이의 차이를 loss로 주어 맞추던 Gradient Matching와 달리, 해당 코드에서는 embed를 통과한 real과 syn 값 차이를 제곱하여 torch.sum하는 과정으로 계산하고 있음을 확인할 수 있다. 논문에서 언급한 더 작은 차원의 공간에서의 mapping을 확인하고 싶었는데, 명시적으로 드러나는 것 같지 않아서 처음에는 찾기 어려웠다. 아마도 view func 통과한 이후, flatten 되는 과정으로 더 낮은 차원 매핑이라고 하는 것 아닐까? 추정 중 . . .
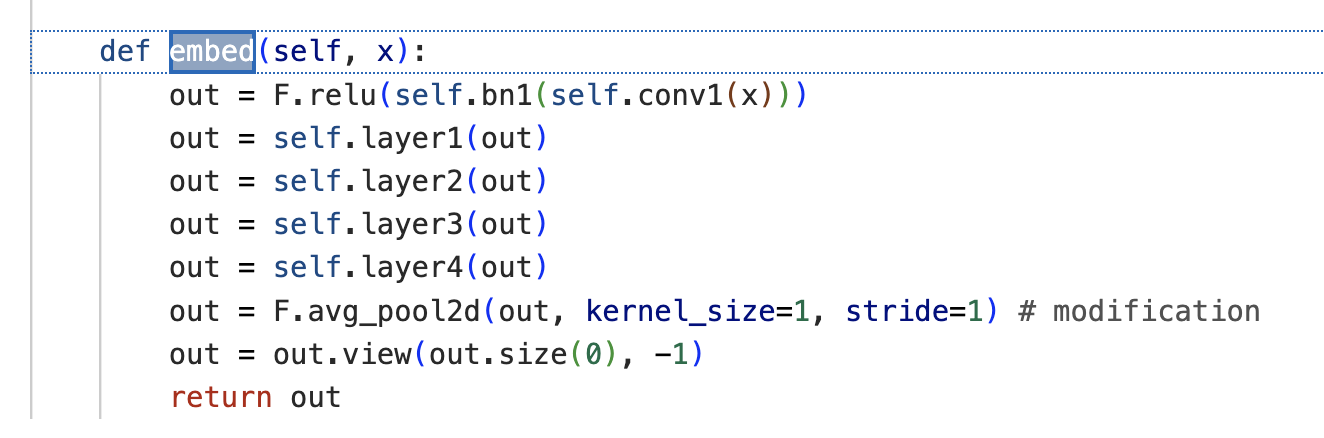
- Network 파일에서, 각 네트워크 별로 정의된 embed 함수를 확인할 수 있다. 이때 ResNet 기반의 embed func은 다른 CNN 기반 네트워크의 embed 함수와 구성이 다른데, 왜 그런 것인지는 잘 모르겠다.
참고 자료
https://github.com/VICO-UoE/DatasetCondensation
GitHub - VICO-UoE/DatasetCondensation: Dataset Condensation (ICLR21 and ICML21)
Dataset Condensation (ICLR21 and ICML21). Contribute to VICO-UoE/DatasetCondensation development by creating an account on GitHub.
github.com
https://www.onurtunali.com/ml/2019/03/08/maximum-mean-discrepancy-in-machine-learning.html
Maximum Mean Discrepancy (MMD) in Machine Learning
Maximum mean discrepancy (MMD) is a kernel based statistical test used to determine whether given two distribution are the same which is proposed in [1]. MMD can be used as a loss/cost function in various machine learning algorithms such as density estimat
www.onurtunali.com
MMD가 무엇인지 모르겠어서, 찾아봤다.
글 후반부에 구체적인 수식과 코드 구현까지 나온다!
- Maximum mean discrepancy (MMD) is a kernel based statistical test used to determine whether given two distribution are the same which is proposed in [1]. MMD can be used as a loss/cost function in various machine learning algorithms such as density estimation, generative models and also in invertible neural networks utilized in inverse problems. As opposed to generative adversarial networks (GANs) which require a solution to a complex min-max optimization problem, MMD criteria can be used as simpler discriminator.
- Main advantages are easy implementation and rich kernel based theory behind the idea that lends itself to a formal analysis. On the other hand, disadvantages are subjectively “mediocre” sample results compared to GANs and the same computational cost overheads regarding kernel based methods when the feature size of the data is reasonable large.
'ArtificialIntelligence > PaperReading' 카테고리의 다른 글
| [Paper reading] NeRF, Representing Scenes as Neural Radiance Fields for View Synthesis (0) | 2023.09.24 |
|---|---|
| [Paper reading] Denoising Diffusion Probabilistic Models (0) | 2023.09.19 |
| [Paper reading] Implicit Neural Representations (0) | 2023.09.18 |
| [Paper reading] Dataset Condensation Keynote (0) | 2023.09.11 |
| [Paper reading] Dataset Condensation reading (0) | 2023.09.11 |